Bài 1 (trang 140 SGK Đại số 11): Dùng định nghĩa xét tính liên tục của hàm số f(x) = x3+2x-1 tại x0=3.
Lời giải:
Hàm số \[f(x)={{x}_{3}}+2x-1\] xác định trên R và \[{{x}_{0}}=3\in \mathbb{R}\]
Ta có: 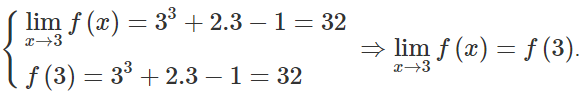
Vậy hàm số đã cho liên tục tại điểm \[{{x}_{0}}=3\]
Bài 2 (trang 141 SGK Đại số 11):
a) Xét tính liên tục của hàm số \[y=g(x)\] tại \[{{x}_{0}}=2\] biết
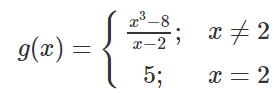
b) Trong biểu thức xác định \[g(x)\] ở trên, cần thay số 55 bởi số nào để hàm số liên tục tại \[{{x}_{0}}=2\]
Lời giải
a) Ta có :
\[\underset{x\to 2}{\mathop{\lim }}\,g\left( x \right)=\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{3}}-8}{x-2}=\underset{x\to 2}{\mathop{\lim }}\,\left( {{x}^{2}}+2x+4 \right)\]
\[={{2}^{2}}+2.2.+4=12\]
\[g\left( 2 \right)=5\]
\[\Rightarrow \underset{x\to 2}{\mathop{\lim }}\,g\left( x \right)\ne g\left( 2 \right)\]
Vì \[\underset{x\to 2}{\mathop{\lim }}\,g(x)\ne g(2)\] nên hàm số \[y=g(x)\] gián đoạn tại \[{{x}_{0}}=2\]
b) Để hàm số \[y=f(x)\] liên tục tại \[{{x}_{0}}=2\] \[\Rightarrow \underset{x\to 2}{\mathop{\lim }}\,g\left( x \right)=g\left( 2 \right)=12\Rightarrow \]ta cần thay số 55 bởi số 12.
Bài 3 (trang 141 SGK Đại số 11): Cho hàm số
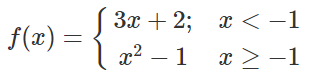
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm sso trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Lời giải:
a. Đồ thị hàm số (hình bên). Từ đồ thị ta thấy số gián đoạn tại x = -1.
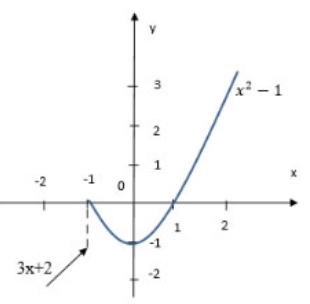
b)
+) Nếu \[x<-1\]; \[f(x)=3x+2\] liên tục trên \[(-\infty ;-1)~\](vì đây là hàm đa thức).
+) Nếu \[~x>-1:~\]\[f(x)={{x}^{2}}-1~\] liên tục trên \[~(-1;+\infty )\] (vì đây là hàm đa thức).
+) Xét tính liên tục của hàm số tại x=−1
Ta có \[\underset{x\to -{{1}^{-}}}{\mathop{lim}}\,f(x)=\underset{x\to -{{1}^{-}}}{\mathop{lim}}\,(3x+2)=3(-1)+2=-1\]
\[\underset{x\to -{{1}^{+}}}{\mathop{lim}}\,f(x)=\underset{x\to -{{1}^{+}}}{\mathop{lim}}\,({{x}^{2}}-1)={{(-1)}^{2}}-1=0\]
Vì \[\underset{x\to -{{1}^{-}}}{\mathop{lim}}\,f(x)\ne \underset{x\to -{{1}^{+}}}{\mathop{lim}}\,f(x)\] nên không tồn tại \[\underset{x\to -1}{\mathop{lim}}\,f(x)\]
Vậy hàm số gián đoạn tại x0=−1
Bài 5 (trang 141 SGK Đại số 11): Ý kiến sau đúng hay sai?
"Nếu hàm số y = f(x) liên tục tại điểm x0 và hàm số y = g(x) không liên tục tại x0, thì y = f(x) + g(x) là một hàm số không liên tục tại x0".
Lời giải:
Ý kiến trên đúng, vì y = h(x) = f(x) + g(x) liên tục tại x0thì h(x) – f(x) = g(x) liên tục tại x0 (theo định lý 2 về hàm số liên tục) trái với giả thiết g(x) không liên tục tại x0.
Bài 6 (trang 141 SGK Đại số 11): Chứng minh rằng phương trình:
a. 2x3 – 6x + 1 = 0 có ít nhất hai nghiệm.
b. cos x = x có nghiệm
Lời giải:
a.
Đặt f(x) = 2x3 – 6x + 1
TXĐ: D = R
Ta có: f(-2) = 2.(-2)3 – 6(-2) + 1 = - 3 < 0
f(-1) = - 2 + 6 + 1 = 5 > 0
f(-2).f(-1) < 0
Mà f(x) là hàm đa thức xác định trên R nên liên tục trên tập R. Do đó f(x) liên tục trên (-2; -1).
Phương trình f(x) = 0 có ít nhất một nghiệm x0 ∈(-2; -1).
Tương tự ta có:
f(-1) = 2(-1)3 – 6(-1) + 1 = 5
f(1) = 2 - 6 + 1 = -3
f(-1).f(1) < 0 nên phương trình có ít nhất một nghiệm x0∈ (-1;1).
Vì các đoạn (-2; -1) và (-1; 1) rời nhau nên các nghiệm nói trên không thể trùng nhau. Vậy phương trình đã cho có ít nhất 2 nghiệm.
b.
Xét hàm số g(x) = x - cos x liên tục trên R, do đó liên tục trên đoạn [- π; π] ta có:
g(- π) = - π - cos (- π) = - π + 1 < 0
g( π) = π - cos π = π - (-1) = π + 1 > 0
g(- π). g( π) <0
Theo định lí 3, phương trình x - cos x = 0 có nghiệm trong (- π; π) tức là cos x = x có nghiệm.