Bài 1 (trang 104 SGK Hình học 11): Cho mặt phẳng (α) và hai đường thẳng a, b. Các mệnh đề sau đây đúng hay sai?
a) Nếu a // (α), b ⊥(α) thì a ⊥b.
b) Nếu a // (α), b ⊥a thì b ⊥(α).
c) Nếu a // (α), b // (α) thì b // a.
d) Nếu a ⊥(α), b ⊥a thì b ⊥(α).
Lời giải:
a) Đúng
b) Sai
c) Sai
d) Sai
Giải thích:
a) a // (α) a // a' (α) (1)
b ⊥(α) b ⊥a' (2)
(1) và (2) a ⊥b
b) Điều này chưa đủ để b ⊥(α)
c)
● a // (α) a // a' (α)
● b // (α) b // b' (α)
a' và b' có thể cắt nhau nên a và b có thể chéo nhau
d) a ⊥(α) và b ⊥a thì b có thể nằm trong mp(α)
Bài 2 (trang 104 SGK Hình học 11): Cho tứ diện ABCD có hai mặt ABC và BCD là hai tam giác cân có chung đáy BC. Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng BC vuông góc với mặt phẳng (ADI)
b) Gọi AH là đường cao của tam giác ADI, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Lời giải:
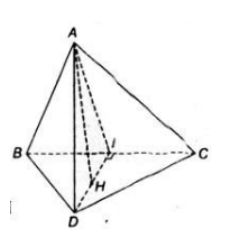
a) ΔABC cân tại A có I là trung điểm của BC (gt)
=> AI vừa là trung tuyến vừa là đường cao của tam giác.
=> AI⊥BC
Tương tự, với ΔBCD cân tại D, I là trung điểm BC
=> DI⊥BC
Ta có: .png)
(Tính chất: đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng)
b) Ta có:
BC⊥(AID), AH∈(AID) (cmt) => BC⊥AH (Tính chất: đường thẳng vuông góc với mặt phẳng thì vuông góc với mọi đường nằm trong mặt)
Ta có: .png)
⇒AH⊥(BCD) (tính chất)
Bài 3 (trang 104 SGK Hình học 11): Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SB = SC = SD. Chứng minh rằng:
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phẳng (SAC).
Lời giải:
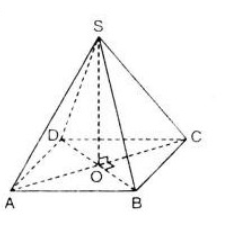
a) Theo giả thiết SA=SC nên tam giác SAC cân tại S
Có: O là giao của hai đường chéo hình bình hành nên O là trung điểm của AC và BD.
Do đó SO vừa là trung tuyến đồng thời là đường cao trong tam giác SAC
=> SO⊥AC (1)
Chứng minh tương tự ta được: SO⊥BD (2)
Từ (1) và (2) ta có: .png)
b) ABCD là hình thoi có AC,BD là hai đường chéo nên AC⊥BD (Tính chất hình bình hành) (3)
Từ (1) và (3) ta có: .png)
Từ (2) và (3) ta có: .png)
Bài 4 (trang 105 SGK Hình học 11): Cho tứ diện OABC có ba cạnh OA, OB và OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng:
a) H là trực tâm của tam giác ABC;
b) \[\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}.\]
Lời giải:
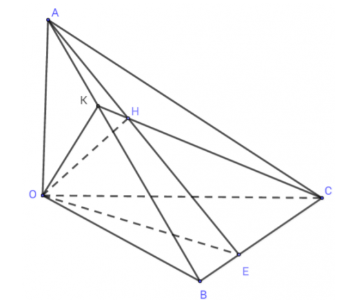
a) H là hình chiếu của O trên mp (ABC) nên OH⊥(ABC)⇒OH⊥BC. (1)
Mặt khác: OA⊥OB, OA⊥OC
⇒OA⊥(OBC)⇒ OA⊥BC (2)
Từ (1) và (2) suy ra BC⊥(AOH)⇒ BC⊥AH. Chứng minh tương tự ta được AB⊥CH
⇒H là trực tâm của tam giác ABC.
b) Trong mặt phẳng (ABC) gọi E=AH∩BC, OH⊥(ABC), AE⊂(ABC)⇒OH⊥AE tại H; tức là OH là đường cao của tam giác vuông OAE.
BC⊥(OAH)⇒BC⊥OE⇒OE là đường cao của tam giác vuông OBC.
Do đó:
\[\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{E}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}+\frac{1}{O{{C}^{2}}}.\]
Bài 5 (trang 105 SGK Hình học 11): Trên mặt phẳng (α) cho hình bình hành ABCD tâm O. Gọi S là một điểm nằm ngoài mặt phẳng (α) sao cho SA = SC, SB = SD. Chứng minh rằng:
a) SO ⊥(α)
b) Nếu trong mặt phẳng (SAB) kẻ SH vuông góc với AB tại H thì AB vuông góc với mặt phẳng (SOH).
Lời giải:
.png)
a) Theo giả thiết: SA=SC nên tam giác SAC cân tại S.
lại có: O là trung điểm của AC nên SO là đường trung tuyến đồng thời là đường cao của tam giác cân SAC nên SO⊥AC
Chứng minh tương tự với SB=SD, O là trung điểm của BD ta có: SO⊥BD
Ta có:
.png)
Vậy SO⊥mp(α) (đpcm)
b) SO⊥(ABCD)⇒SO⊥AB (1)
Mà SH⊥AB (gt) (2)
Từ (1) và (2) ta có
.png)
Bài 6 (trang 105 SGK Hình học 11): Cho hình chóp S.ABCD có đáy là hình thoi ABCD và có cạnh SA vuông góc với mặt phẳng (ABCD). Gọi I và K là hai điểm lần lượt lấy trên hai cạnh SB và SD sao cho SI/SB = SK/SD .
Chứng minh:
a) BD ⊥ SC
b) IK ⊥mp(SAC)
Lời giải:
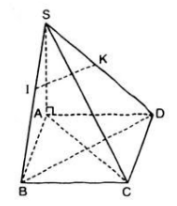
a) ABCD là hình thoi nên \[AC\bot BD\] (1)
Theo giả thiết: \[SA\bot (ABCD)\Rightarrow SA\bot BD\] (2)
Từ (1) và (2) suy ra \[BD\bot (SAC)\]\[\Rightarrow BD\bot SC\]
b) Theo giả thiết \[\frac{SI}{SB}=\frac{SK}{SD}\] theo định lí Ta-lét ta có \[IK//BD\]
Theo a) ta có: \[BD\bot (SAC)\Rightarrow IK\bot (SAC)\]
Bài 7 (trang 105 SGK Hình học 11): Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại B. Trong mp(SAB), kẻ AM vuông góc với SB tại M. Trên cạnh SC lấy điểm N sao cho SM/SB = SN/SC.
Chứng minh rằng:
a) BC ⊥ (SAB), AM ⊥ (SBC)
b) SB ⊥ AN
Lời giải:
.png)
a) \[SA\bot (ABC)\Rightarrow SA\bot BC\] (1)
Tam giác ABC vuông tại B nên \[BC\bot AB\] (2)
Từ (1) và (2) suy ra \[BC\bot (SAB)\]
\[BC\bot (SAB)\] nên \[BC\bot AM\] (3)
\[AM\bot SB\] (giả thiết) (4)
Từ (3) và (4) suy ra \[AM\bot (SBC)\]
b) \[AM\bot (SBC)\] nên \[AM\bot SB\] (5)
Giả thiết \[\frac{SM}{SB}=\frac{SN}{SC}\] nên theo định lí ta lét ta có: \[MN//BC\]
Mà BC⊥SB (do BC⊥(SAB) do đó MN⊥SB (6)
Từ (5) và (6) suy ra SB⊥(AMN) suy ra SB⊥AN
Bài 8 (trang 105 SGK Hình học 11): Cho điểm S không thuộc mặt phẳng (α) có hình chiếu trên (α) là điểm H. Với điểm M bất kì trên (α) và không trùng với H, ta gọi SM là đường xiên và đoạn HM là hình chiếu của đường xiên đó.
Chứng minh rằng:
a) Hai đường xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;
b) Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại, đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Lời giải:
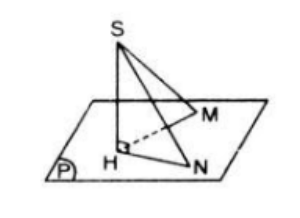
Gọi SN là một đường xiên khác.
a) Xét hai tam giác vuông SHM và SHN có SH cạnh chung.
- Nếu SM=SN⇒∆SHM=∆SHN(c−g−c)
⇒HM=HN.(2 cạnh tương ứng)
- Ngược lại nếu HM=HN thì ∆SHM=∆SHN(c−g−c)
⇒SM=SN. (2 cạnh tương ứng)
Vậy: Hai đường thẳng xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau.
b) Xét tam giác vuông SHM và SHN có SH cạnh chung.
- Giả sử SN>SM
Áp dụng định lí Pytago vào hai tam giác vuông SHM và SHN ta được:
\[H{{M}^{2}}=S{{M}^{2}}-S{{H}^{2}}\]
\[H{{N}^{2}}=S{{N}^{2}}-S{{H}^{2}}\]
⇒HN>HM.
- Ngược lại: giả sử HN>HM
Áp dụng định lí Pytago vào hai tam giác vuông SHM và SHN ta được:
\[S{{M}^{2}}=H{{M}^{2}}+S{{H}^{2}}\]
\[S{{N}^{2}}=H{{N}^{2}}+S{{H}^{2}}\]
⇒SN>SM.
